1/31/2005

return to index page

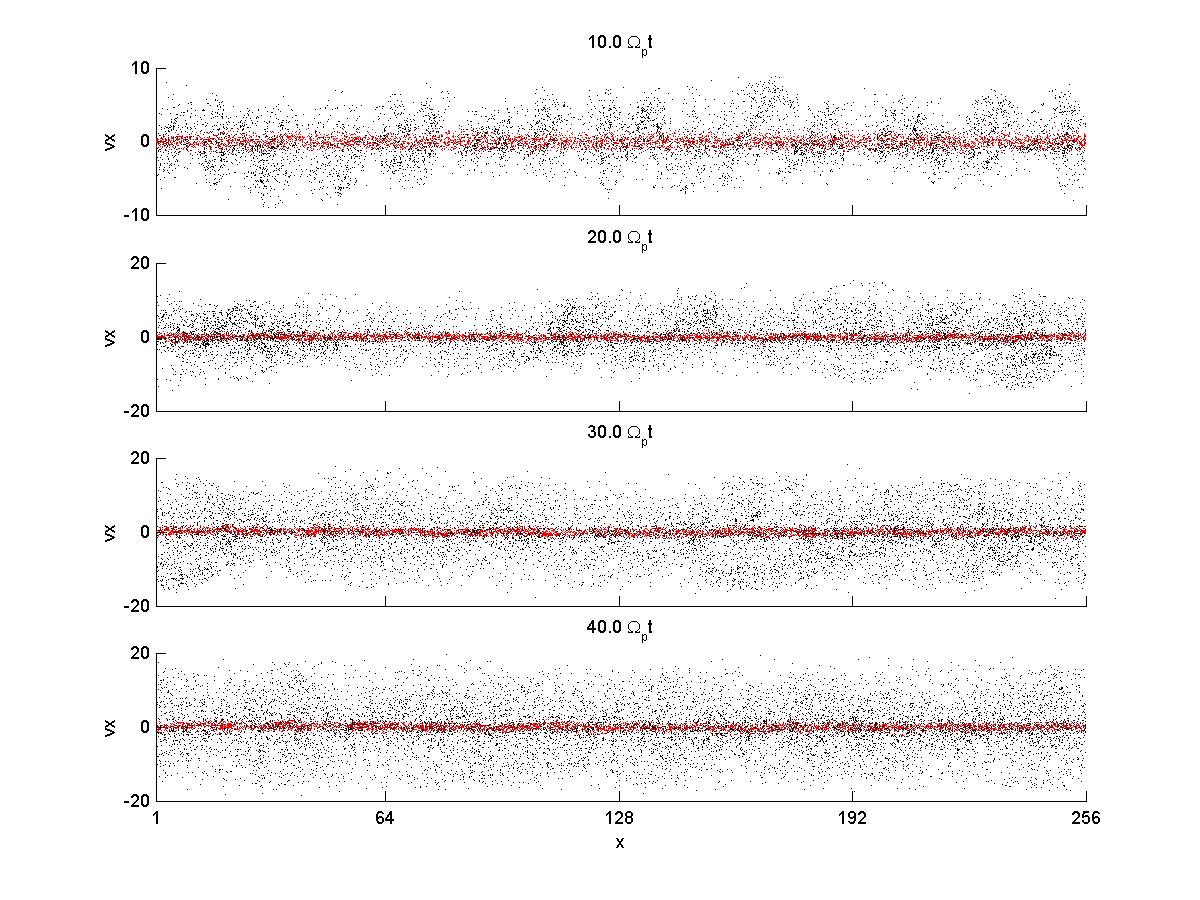
This is the first run for the case of perpendicular pickup. The magnetic field is aligned with the simulation axis, x,and the ion beam/core is along z. The core ions are initialized as cold maxwellian, while the beam are initialized as a ring beam with perpendicular velocity of 10 vA and are injected uniformly across the simulation axis.

values in input.h:
ntimes= 400 dtwci= 0.1 nx=256 xmax=256 wpiwci=10000. nsp = 2 nspec(1)=5120 nspec(2)= 10240 vbspec(1)=0. vbspec(2)=0. vbperp(1)= -0.15 vbperp(2)=9.85 dnspec(1)=1.0 dnspec(2)=0.02 btspec(1)=1.0 btspec(2)=1.0 anspec(1)=1. anspec(2)=1. wspec(1)=1.0D0 wspec(2)=1.0D0 add_no(1) = 0. add_no(2) = 2.0e-5*nspec(1)*1200 bete=1. resis=0. theta=0. iemod=0

I use vbspec to be the beam drift velocity parallel to B and vbperp as the velocity perp to B. I modified the code such that the beam and B are fixed perpendicular to each other (don't use theta). add_no is the injection rate.

The injected ring beam is initialized:
vx = thermal velocity + beam parallel velocity (vbspec = 0)
vy = ring distribution (w/ thermal spread)
vz = ring distribution (w/ thermal spread) + beam perpendicular velocity (vbperp)


Here are the results:

1) Phase Space (red = background fixed, black = beam injected)
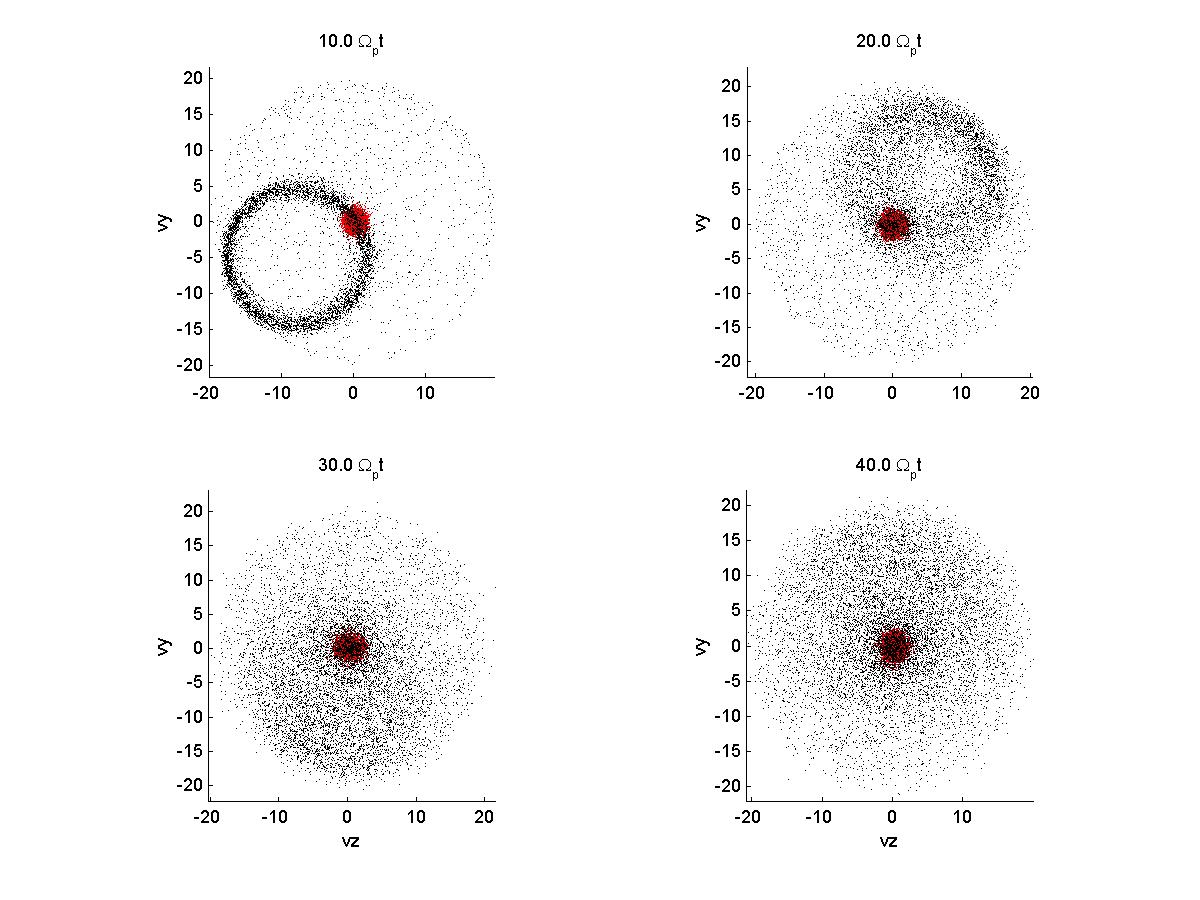
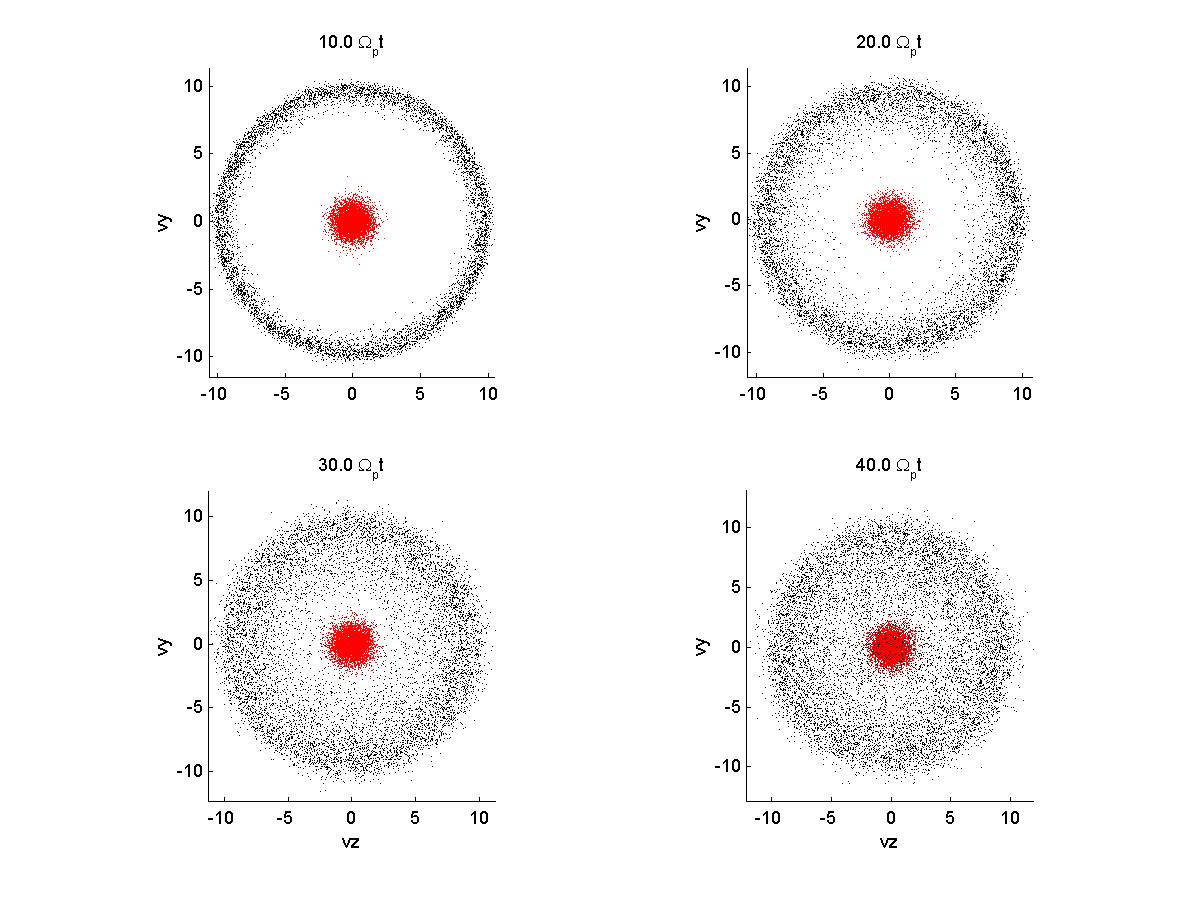
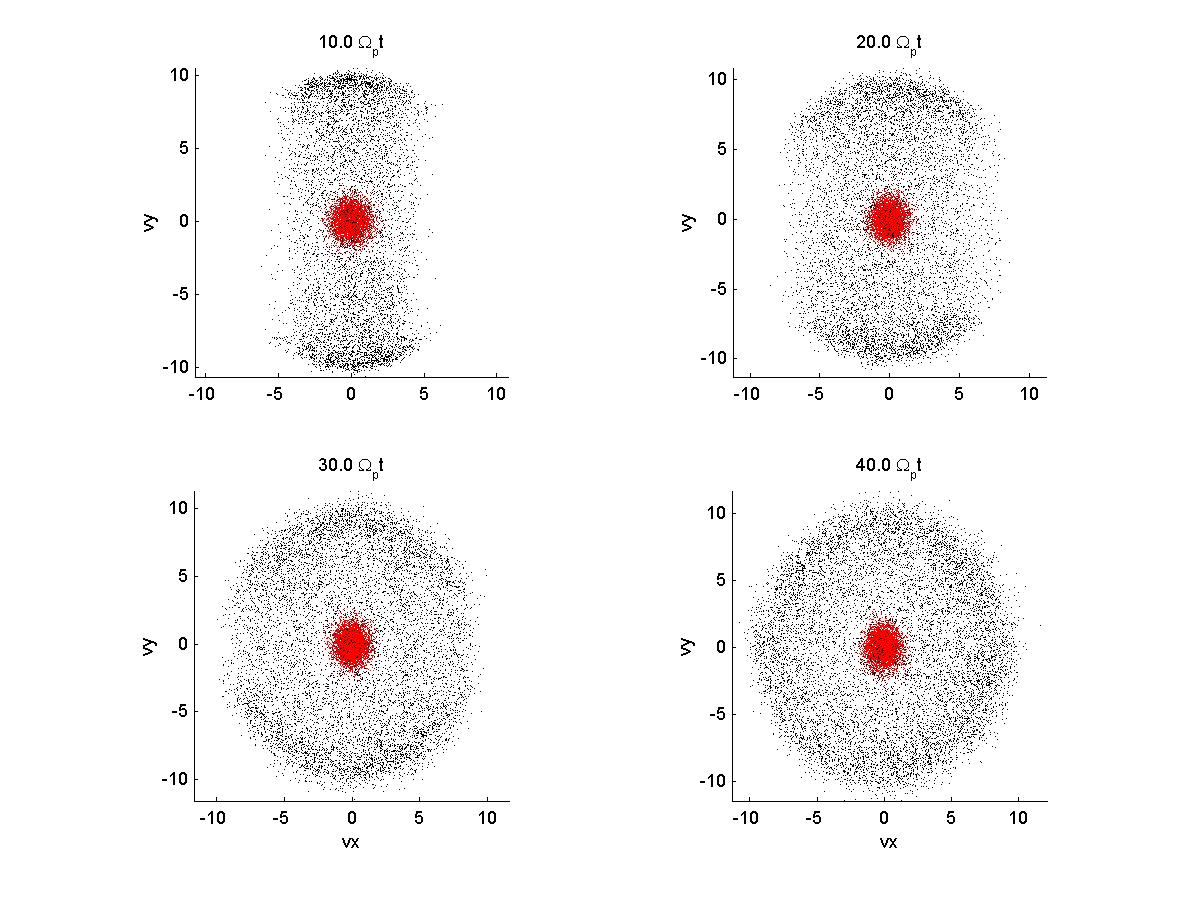
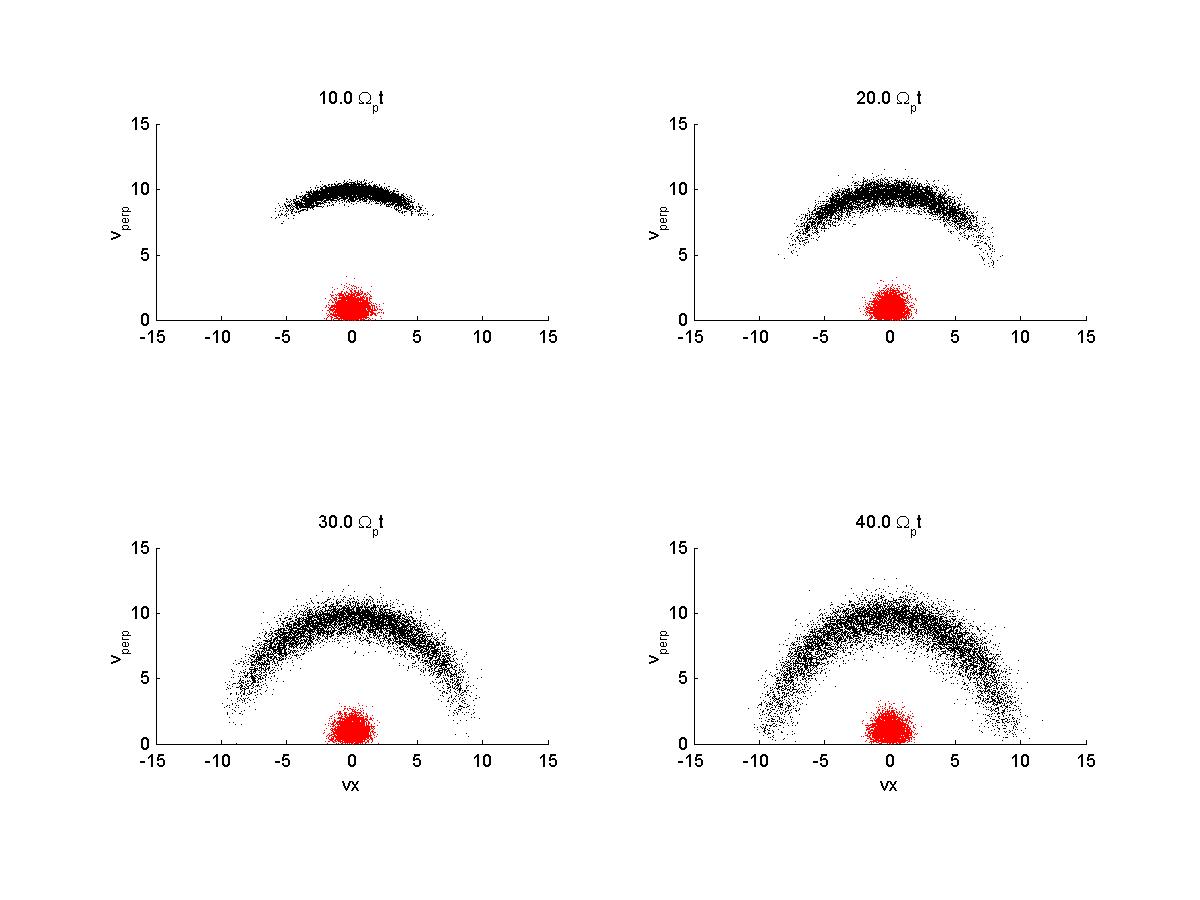
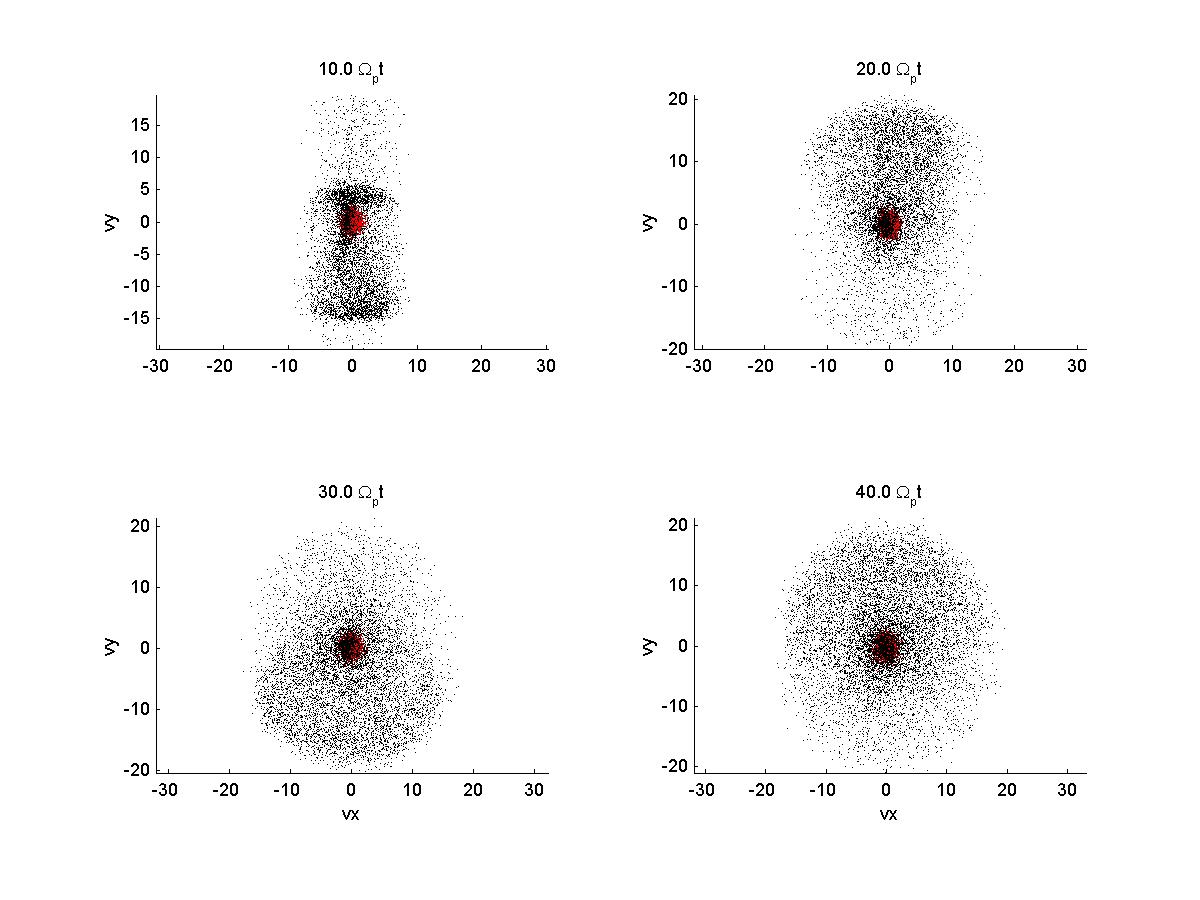
2a) Velocity Space	2b) Velocity Space
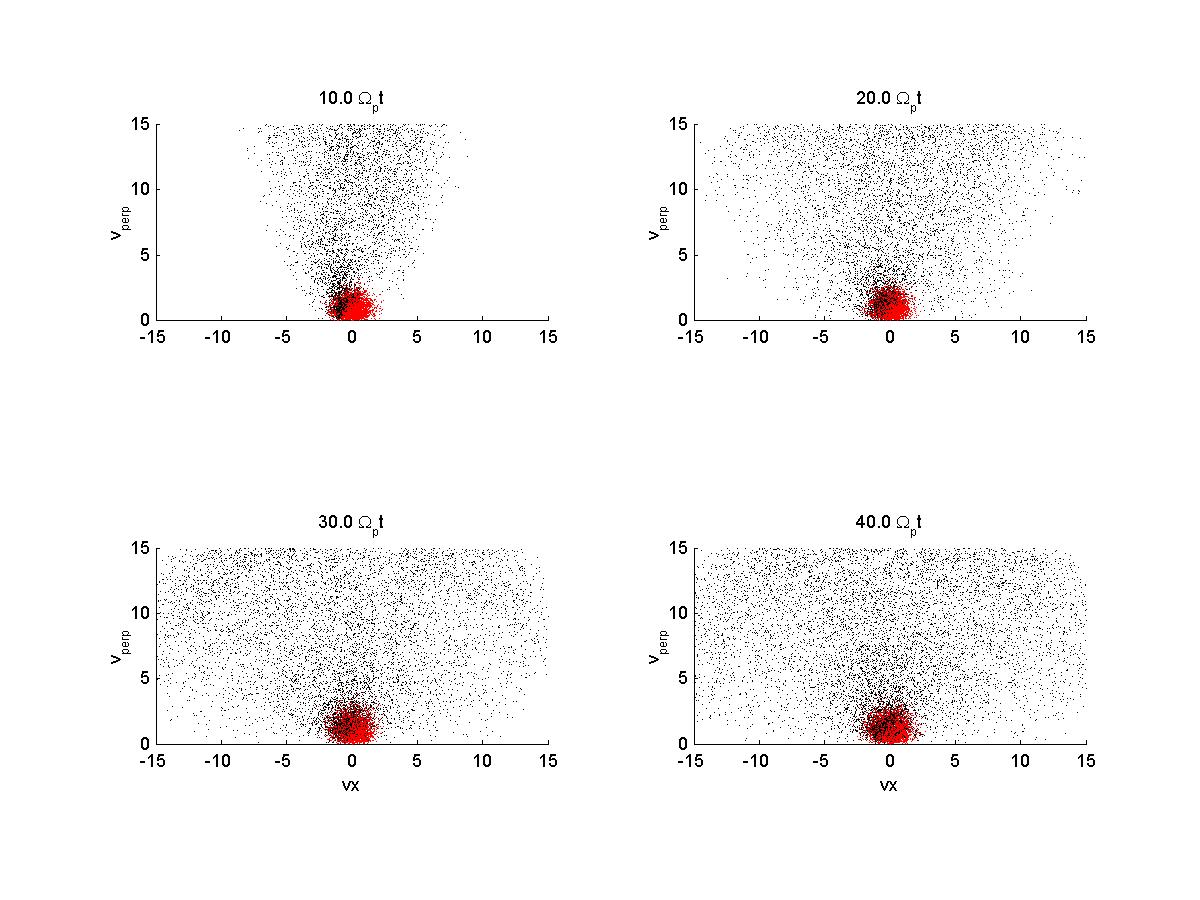
2c) Velocity space
*note that when the variable vbperp = 0 and the ring perp veloc is kept at 10 vA, the ring is centered around the thermal distribution in vy-vz. I assume this difference is from the frame of reference now with the drifting beam. See below:
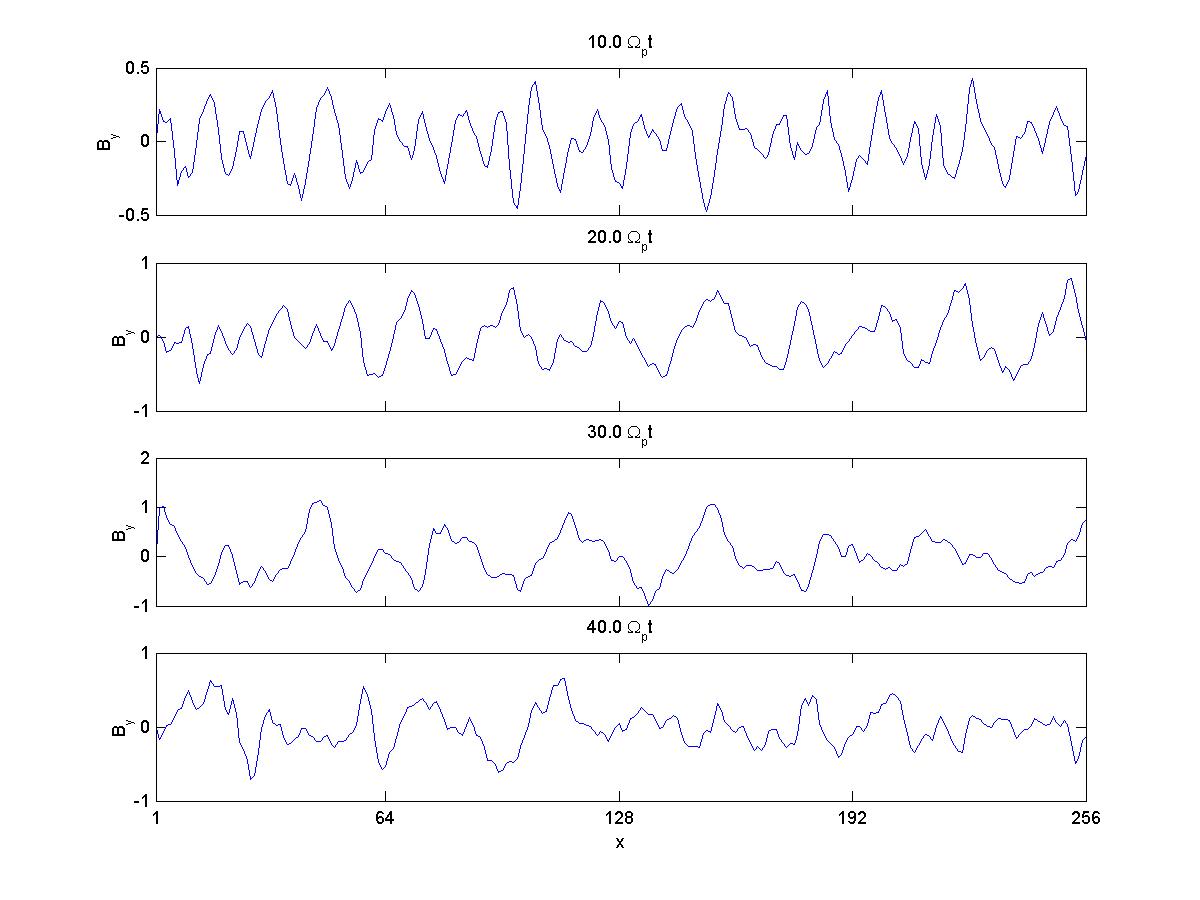
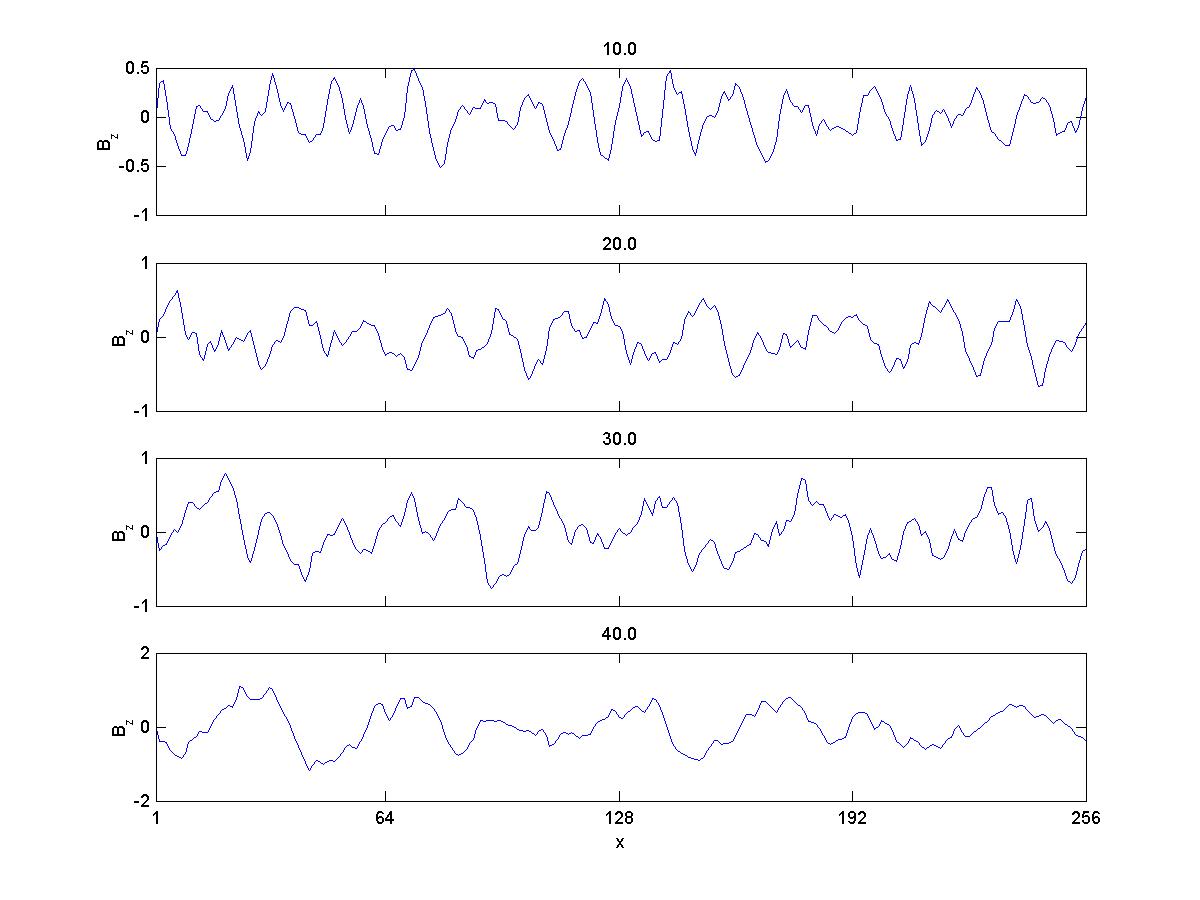
3a) By	3b) Bz
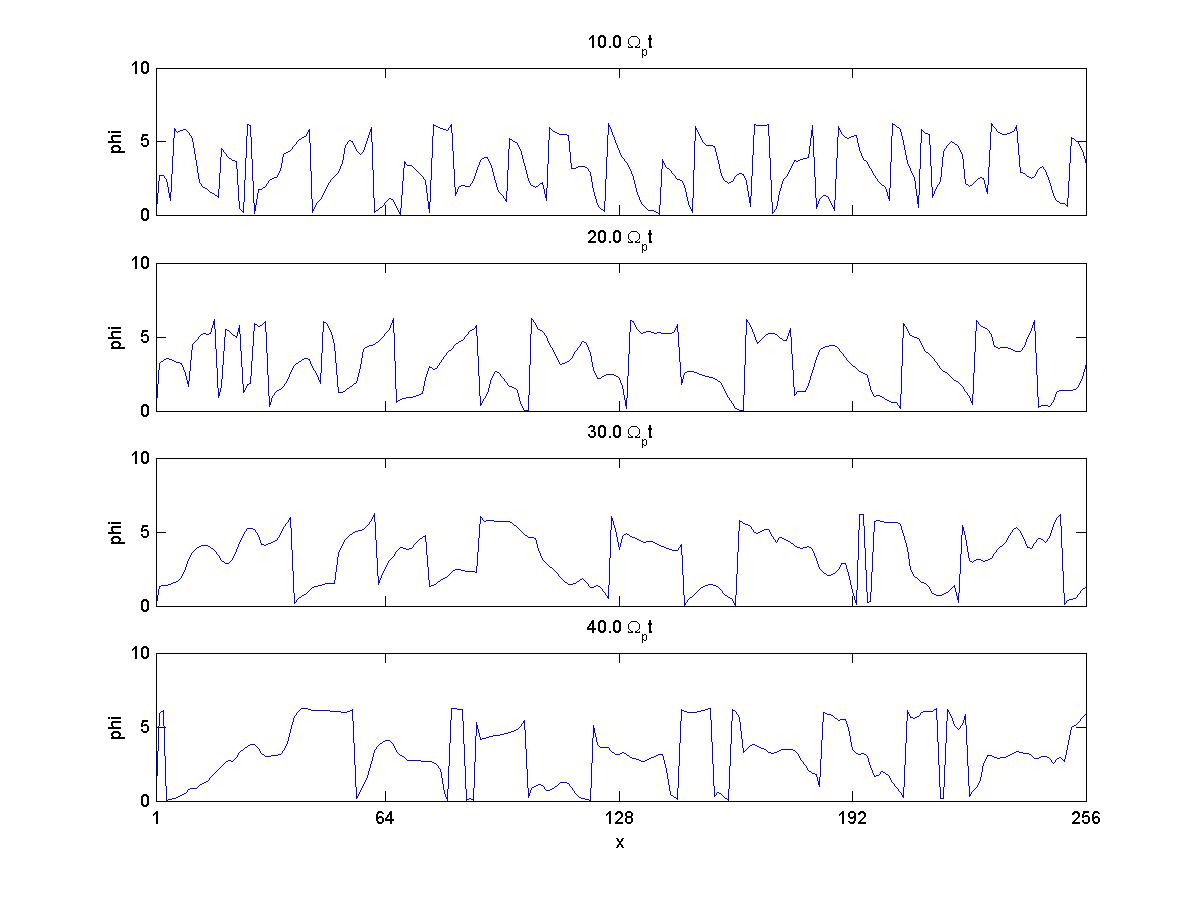
3c) Phi
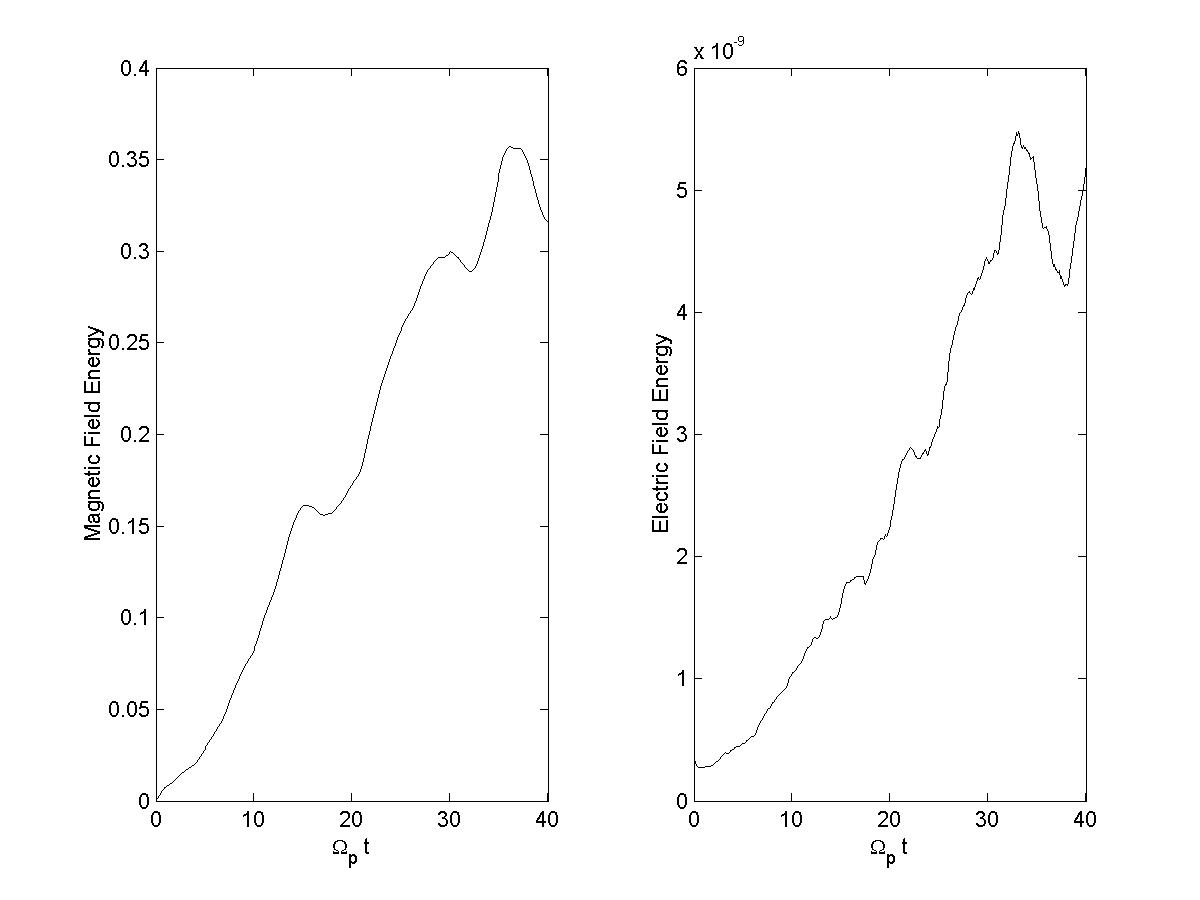
4) B field energy
5) Fourier modes

return to index page