(red = background fixed, black = beam injected)

return to index page
Here are the results for my attempt to copy the results from "The development of shell-like distributions from newborn cometary ions" by Gary, Hinata, Madland and Winske, GRL, 1986 (aka the first part from the continuation paper, "Computer simulations of two- pickup-ion instabilities in a cometary environment" by Gary, Madland, Omidi and Winske, JGR 1988).
The code is set up with simulation axis x; beam/core and B0 are along x. Ions are injected
randomly along x with constant injection rate.
values in input.h:
ntimes= 4096
dtwci= 0.2
nx=32
xmax=128
wpiwci=10000.
nsp = 2
nspfix = 1
nspinj = 1 (// 2 SPECIES, 1 FIXED AND 1 INJECTED; VALUES LISTED IN THAT ORDER)
nspec(1)=5000
nspec(2)=5000
vbspec(1)=0.0
vbspec(2)=10.0
dnspec(1)=1.0
dnspec(2)=0.0
btspec(1)=1.0
btspec(2)=1.0
anspec(1)=1.
anspec(2)=0.01
wspec(1)=1.0D0
wspec(2)=1.0D0
add_no(1) = 0.
add_no(2) = 2.0e-5*nspec(1) (// INJECTION: ADD_NO IN UNITS OF CYCLOTRON FREQ; 0 = NOT INJECTED)
bete=1.
resis=0.
theta=0.
iemod=0
Questions/Comments:
(1) vbspec: For a zero-drift maxwellian, I used vbspec(1) = 0; and since vob = 10vA, vbspec(2) = 10
(2) dnspec: For zero current condition, then dnspec(1) = 1.0, and dnspec(2) = 0
(3) anspec: These values were not given in the paper, however Gary et al. 1988 shows the injected ions
to initially occupy a very small region of velocity space. So I set anspec(2) = 0.01.
(4) add_no: This is in units of wci. The papers showed that dn_inj/dt = 2.0D-5*nc where nc = 5000.
This means that for the given timestep, 1 ion is injected every 50 timesteps --> 82 ions injected during the run.
(5) This injection rate is too small --> the figures in the paper show more than 80 ions added during the
simulation. I think I must have misunderstood what the right injection rate is.
Here are the results:
|
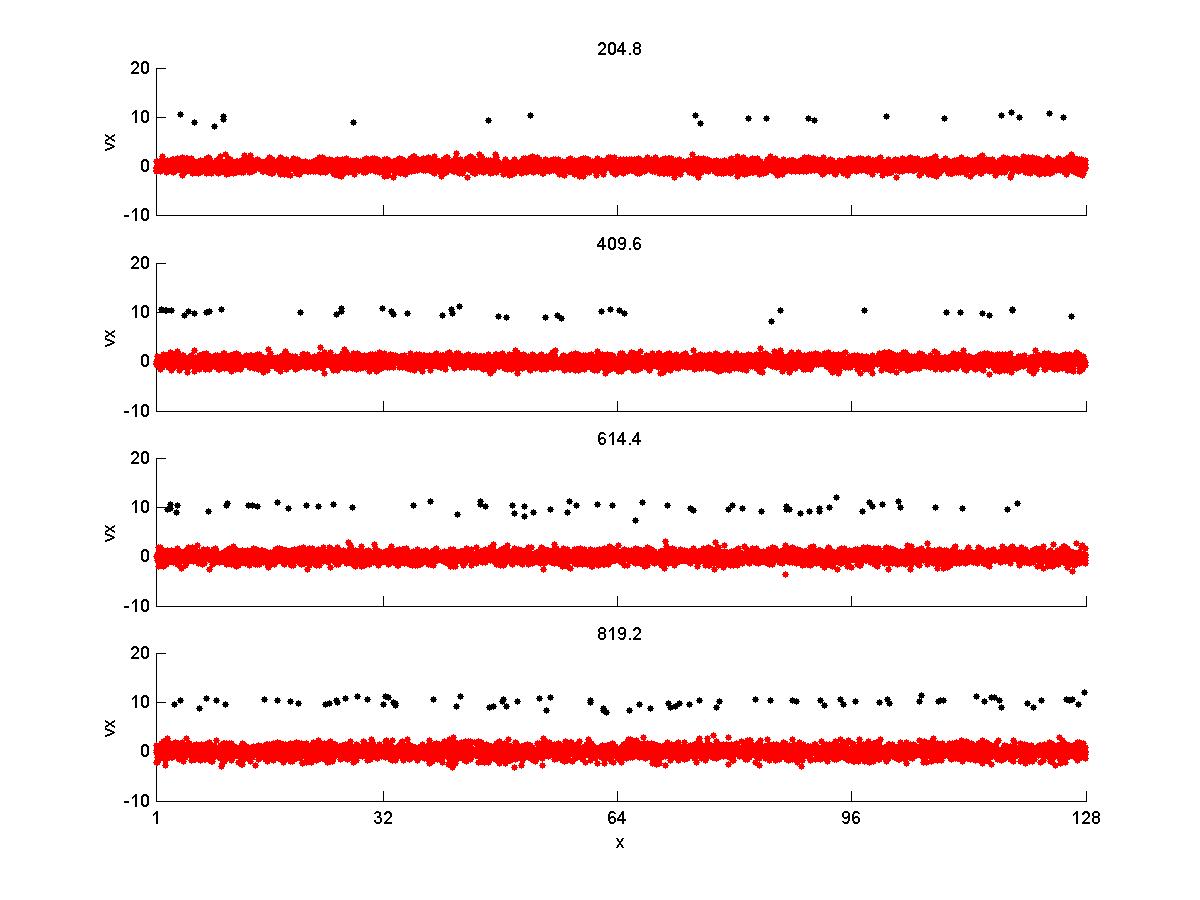
1) Phase Space (red = background fixed, black = beam injected) 
| |
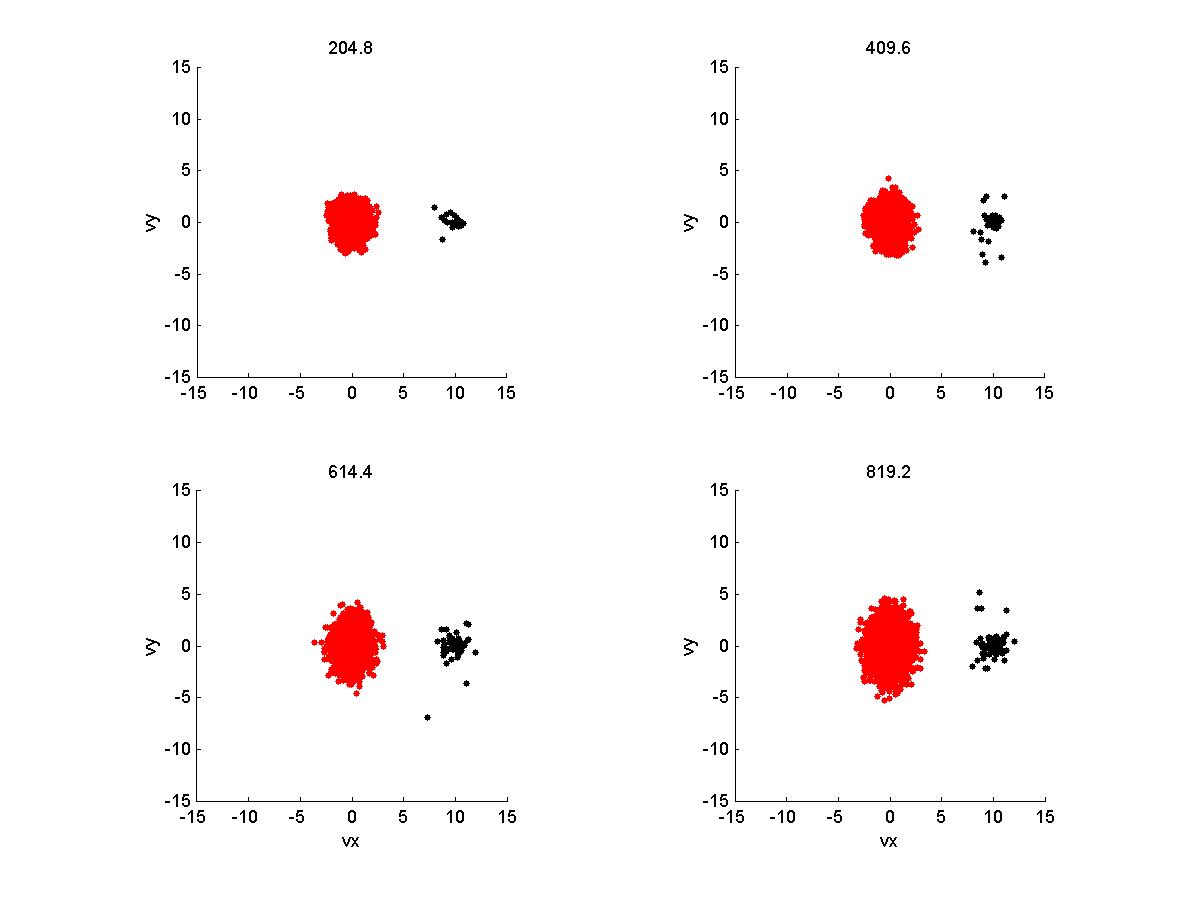
2a) Velocity Space 
|
2b) Velocity Space 
|
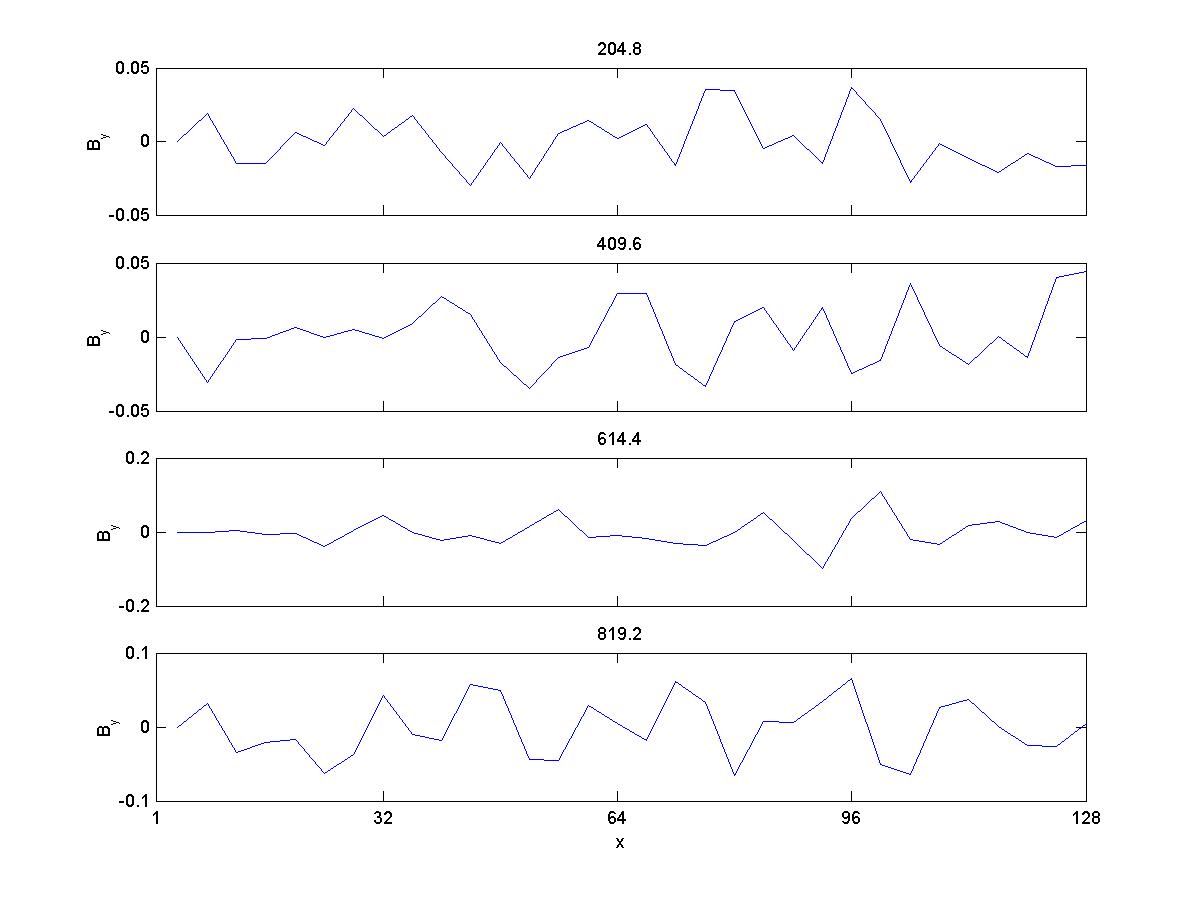
3a) By
|
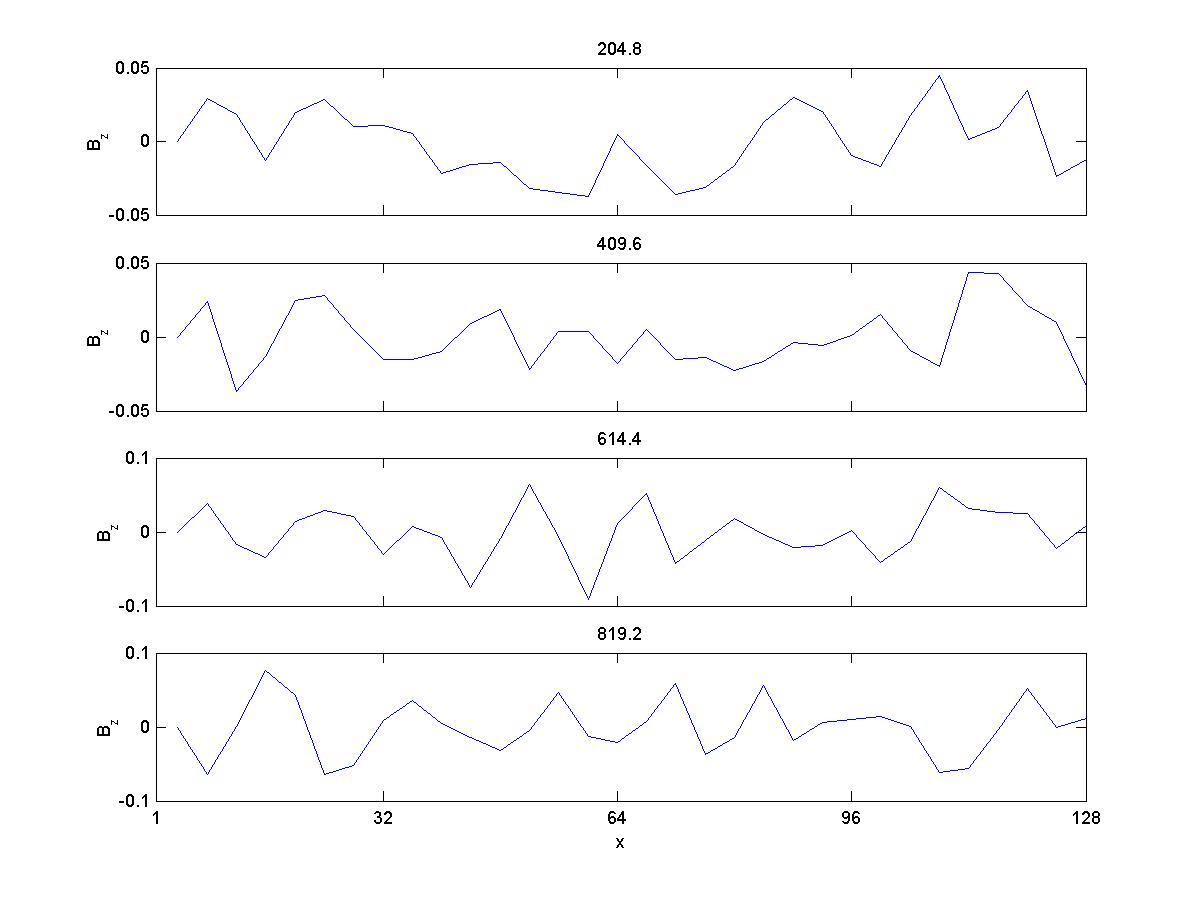
3b) Bz
|
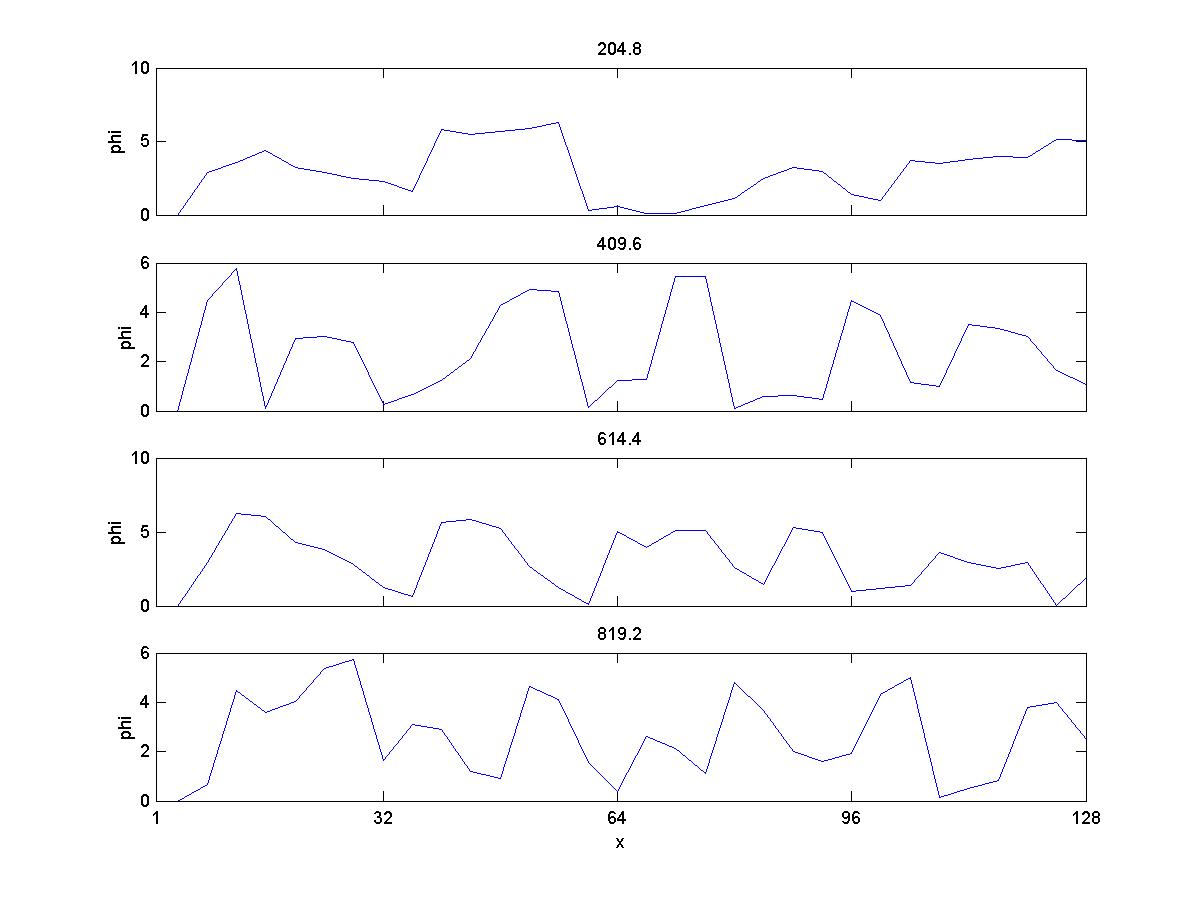
3c) Phi
| |
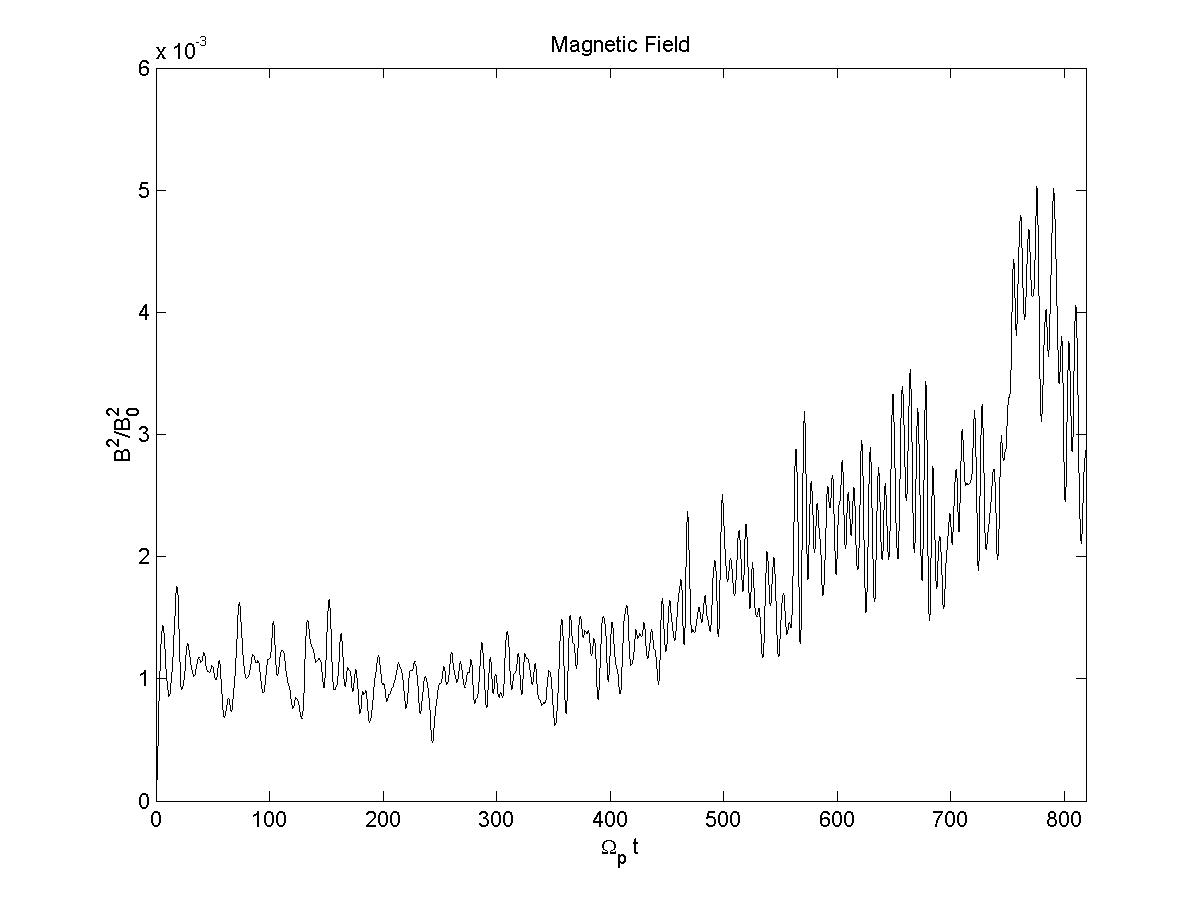
3d) B field energy 
|
As you see, the there is no discernible wave-particle interaction. However, when the injection rate is
increased by a factor of 20,
|
1) Phase Space (red = background fixed, black = beam injected) 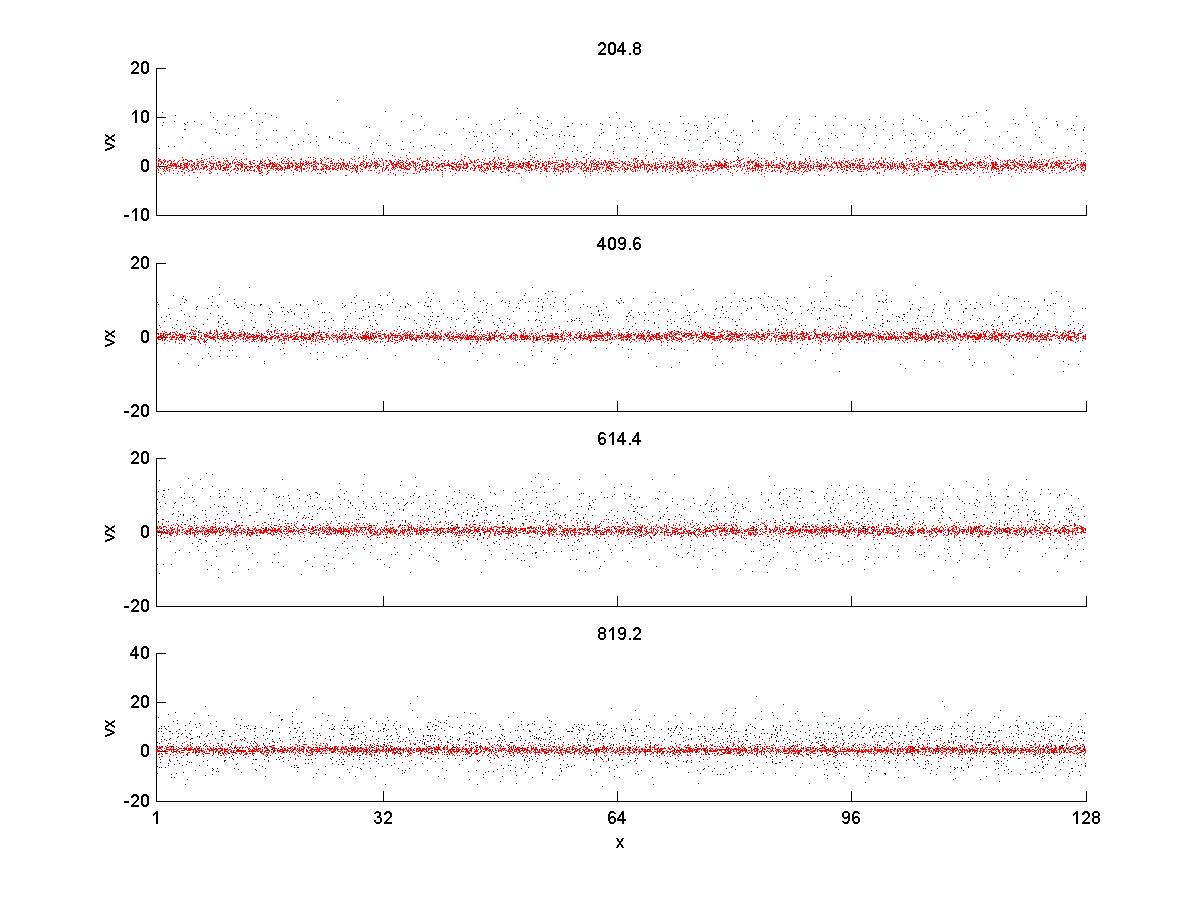
| |
2a) Velocity Space 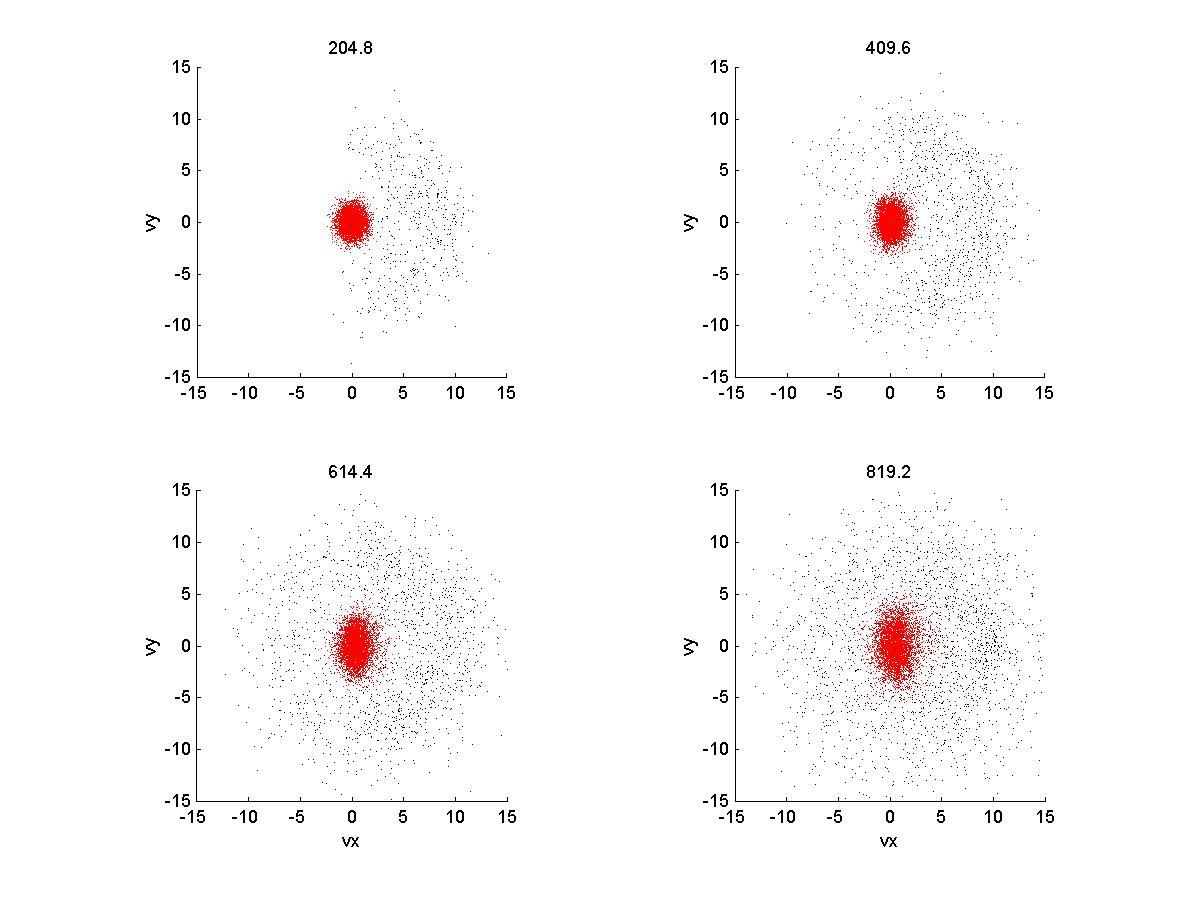
|
2b) Velocity Space 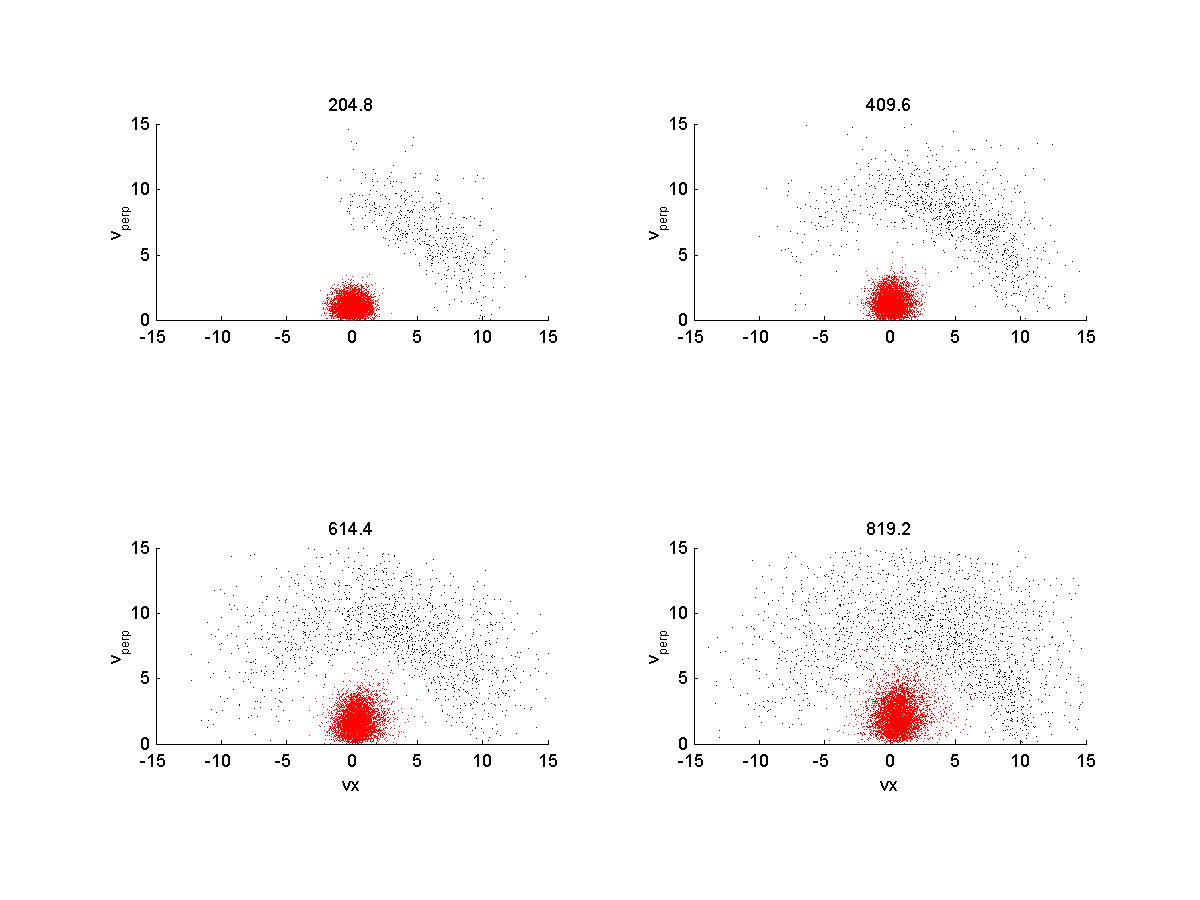
|
3a) By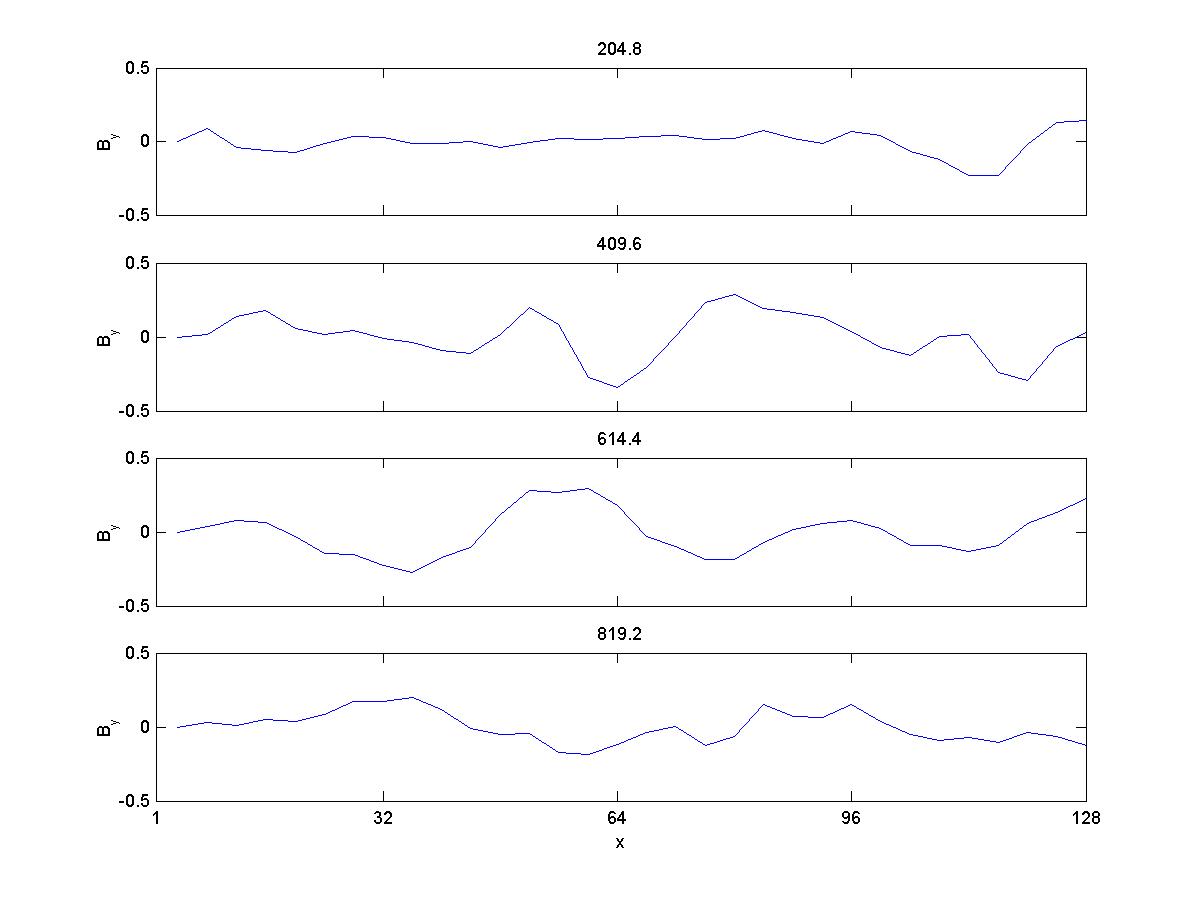
|
3b) Bz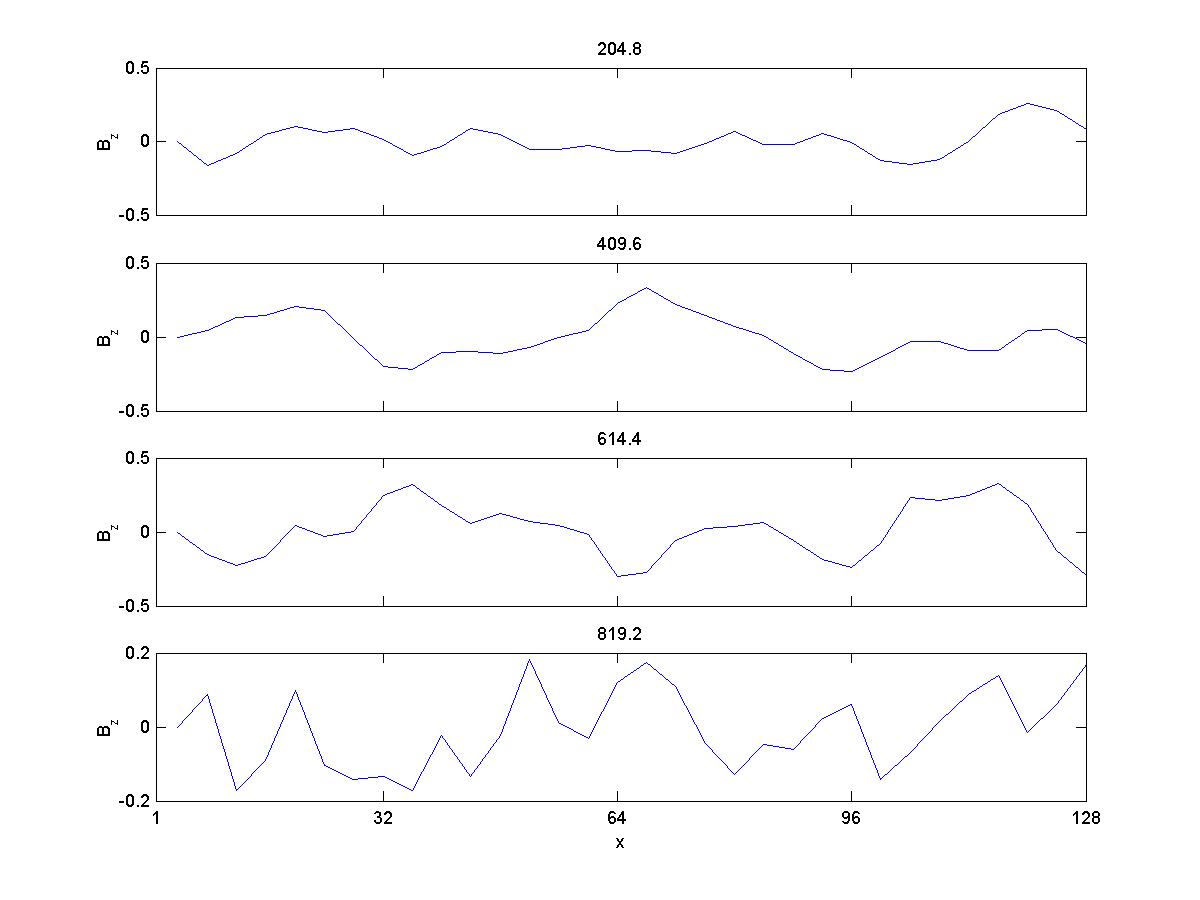
|
3c) Phi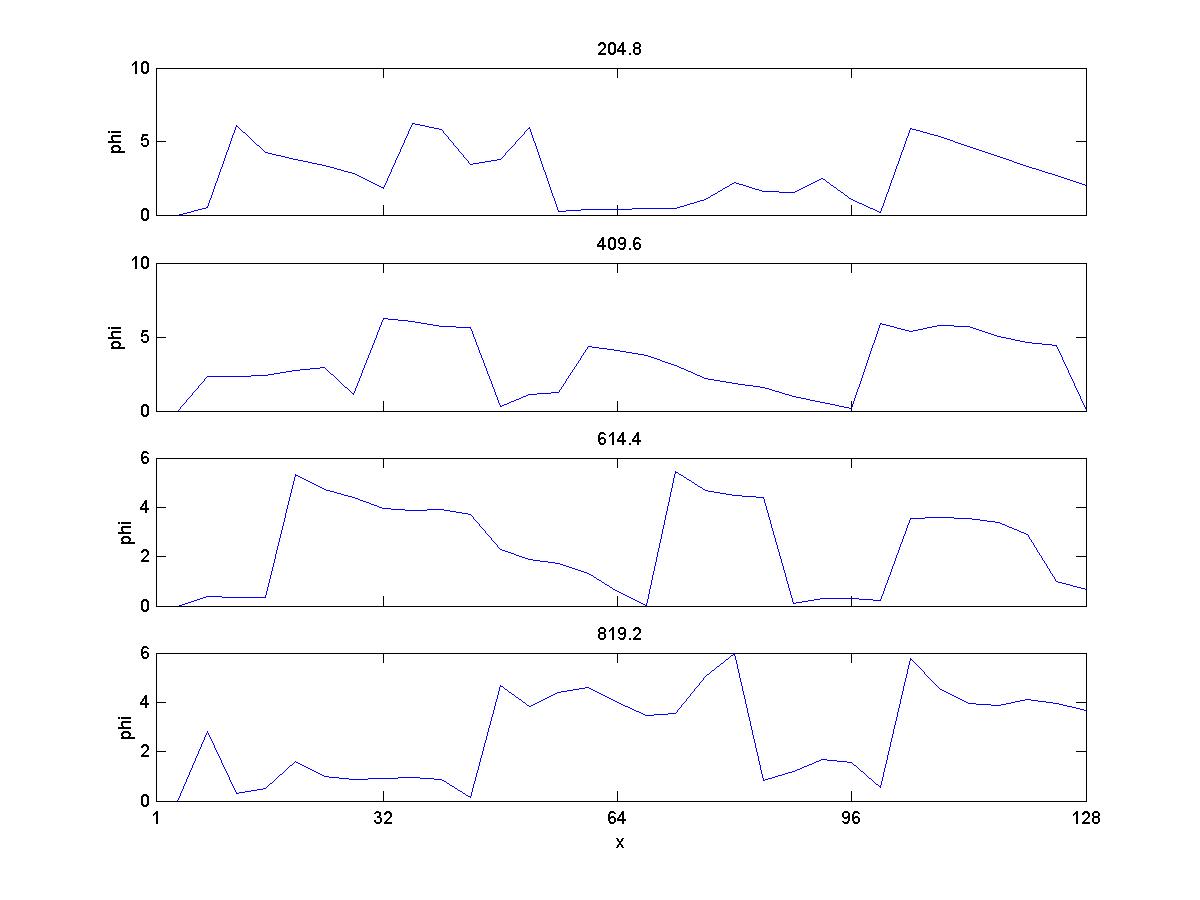
| |
3d) B field energy 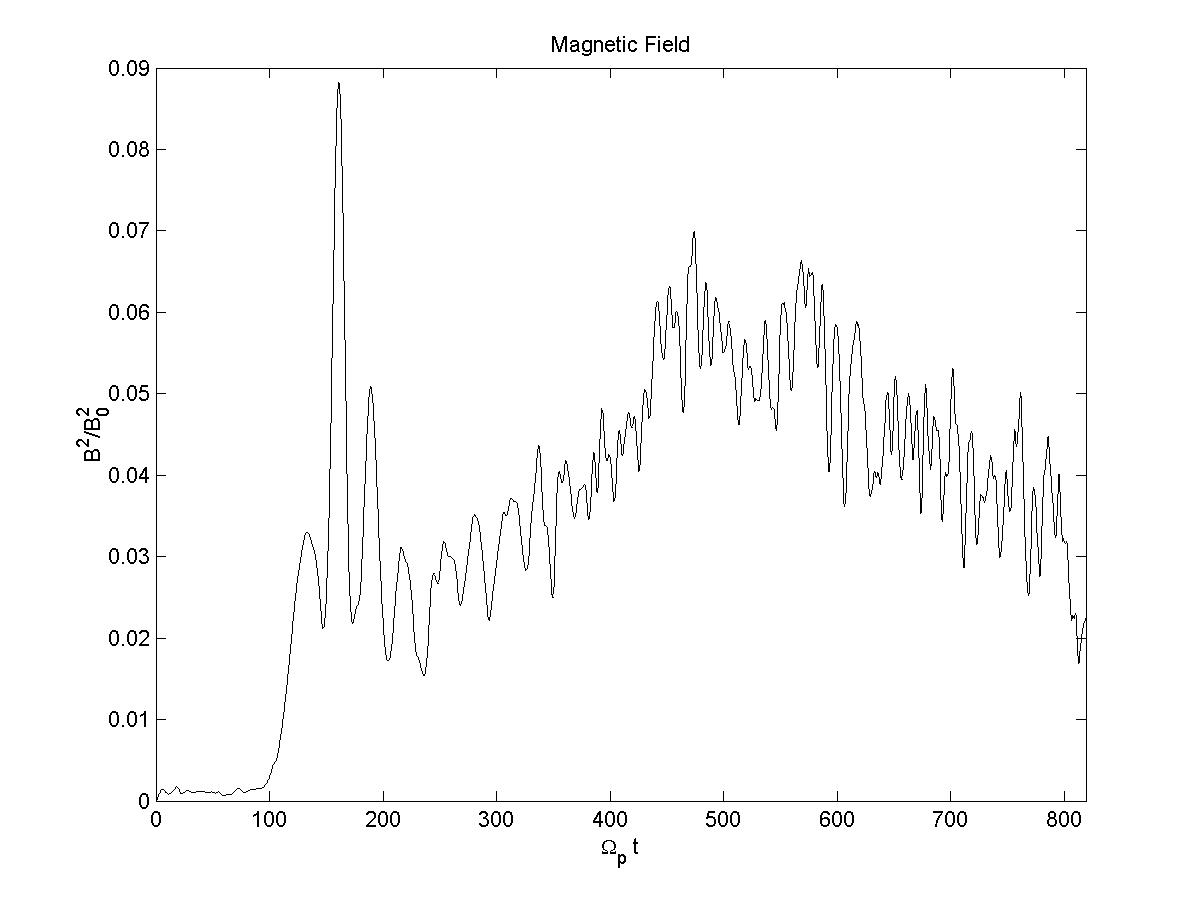
|
So, here the results are qualitively comparable to Gary et al 1986, except for the magnetic energy. Ion velocities also exhibit a larger spread than they do in the paper, and with higher magnitudes. When I try to copy the conditions in Gary et al 1988, with a larger timestep and longer running time, the velocities increase greatly and the simulation crashes (I believe) due to violation of courant condition.
return to index page